Hear the Earth's call of gravity.
Attach weights to a string in equal distances.
One quick option is…
…to use paper clips and nuts.
Then hold the string up and listen as it falls.
www.sciensation.org | Ciênsação hands-on experiments are published as Open Educational resources under a Creative Commons Attribution-ShareAlike 4.0 International License.
Hear the Earth's call of gravity.
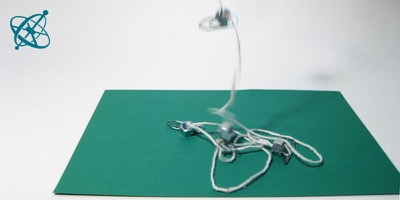
Attach weights to a string in equal distances.
One quick option is…
…to use paper clips and nuts.
Then hold the string up and listen as it falls.
Free falling
The gravitational force, which Newton held responsible for apples falling on him, accelerates everything towards the center of the Earth. With this experiment your students can hear this acceleration g as an increasing beat. And they can demonstrate that they understand the underlying laws of physics – if they manage to modify the setup so that it generates a constant beat.
Listen to the gravitational acceleration.
Translating mathematical models into practical solutions.
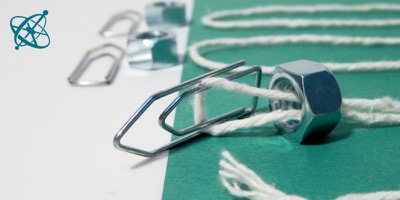
Weights that can be easily attached to the string
Ruler
Have for each group a string of 2 m length and 6 weights which can be easily attached to it. The nuts and paperclips seen in the pictures are merely a suggestion.
Listen to the sound made by the falling weights.
1. Why is the beat increasing?
2. At what distances would you need to attach the weights in order to obtain a constant beat?
The moment you release the string, what downward speed do the weights have?
› None.
Does the first and the last weight hit the ground at the same velocity?
› No, the last one has been accelerating for longer and therefore hits the ground at a higher velocity.
How far does an object fall in a given time?
› From Newtons laws we can deduce that h = 0.5 g t2.
If you want always the same time t between two weights hitting the floor, what distances h need the weights to be apart?
› The distances increase as the square of the number of each weight: h1 = k 12, h2 = k 22,..hn = k n2, where k can be any constant, e.g. k = 5 cm.
The weights accelerate while they fall. Each weight therefore reaches the ground with a higher velocity than the one before, requiring less time to cover the distance between two weights. Thus the time between two weights hitting the ground becomes shorter and an observer hears an increasing beat.
In order to generate a constant beat, not the distances between weights, but the time between two weights hitting the floor has to be constant. Since h ~ t2, the distances have to increase with the square of the weight's number n, i.e. hn~ n2. One possible solution is to attach the weights at distances of 5 cm, 20 cm, 45 cm, 80 cm, 125 cm, and 180 cm.