What is the half-life of a die?
Roll the dice and pick out all the 6's.
After about 4 runs, half of the dice are out.
The 2nd half then takes a bit longer.
www.sciensation.org | Ciênsação hands-on experiments are published as Open Educational resources under a Creative Commons Attribution-ShareAlike 4.0 International License.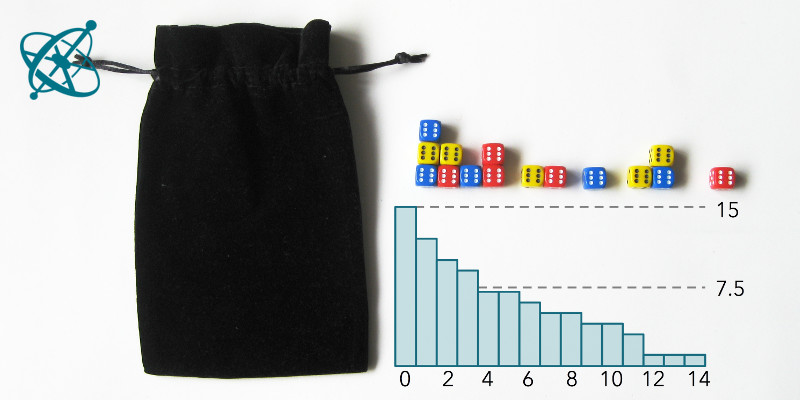
What is the half-life of a die?
Roll the dice and pick out all the 6's.
After about 4 runs, half of the dice are out.
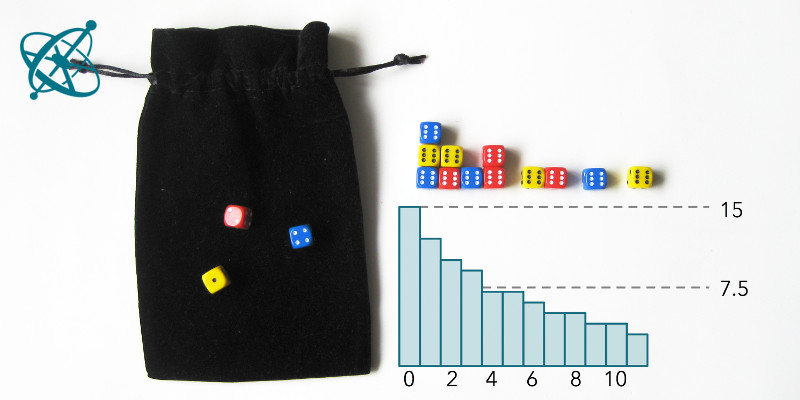
The 2nd half then takes a bit longer.
Dice half-life
Marie and Pierre Curie observed radioactive decay as a glow in their darkened laboratory. It is NOT recommended to repeat this experiment with your students!
Instead, let your students explore the law of radioactive decay with a bag of dice. This is faster, easier to understand and much healthier.
The half-life of a radioactive decay depends only on the probability of an individual atom to decay in a given time period.
Hand out to each group of students at least 10 dice. To show that the half-life does not depend on the number of dice you start with, it is recommended to give each group a different number of dice.
Before rolling the dice, note down the number of dice you start with. At each cast, remove the dice with a '6' facing up and record the number of remaining dice. Repeat until all dice are removed. Then visualize your results in a graph.
1. After how many casts have you removed half of the dice? Compare your result with that of other groups.
2. What determines the number of casts it takes on average to remove half of the dice, and how would you estimate it?
What is the probability of a die NOT to land with a '6' facing up?
› The probability is 5/6.
Assuming a great number of dice and many runs, how many dice should remain on average after two casts?
› After the first cast only 5/6th of the dice remain, of which in the second cast again 5/6th are left. So in total N0 * 5/6 * 5/6 or about 69%.
With some exceptions, groups will find that after 4 rounds at least half of the dice are removed. However, it takes significantly longer until all dice have landed with a '6' facing up.
Since in each run 5/6 remain, the average fraction of remaining dice after n runs is (5/6)n. The half-life can be estimated by setting this equal to 1/2:
(5/6)n=0.5
n=lg(0.5)/lg(5/6) ≅ 3.8
After each group individually has evaluated its record, you can combine results by summing up the remaining dice of all groups after each cast and visualize it in one graph (e.g. using Open Office Calc). In this summary graph, both the exponential decay and the half-life of about 4 runs should be clearly visible.
Just to be accurate: The half-life in this dice experiment differs slightly from the 'true' half-life for radioactive decay. In a radioactive decaying material, nuclei can decay at any time, while the decay in the dice experiment takes place at discrete events, i.e. each cast. The small, yet notable difference in the resulting half-life is explained in detail by Murray and Hart.