Measure the spectral bands of a light source…
…with this open spectrometer and…
…some simple math.
www.sciensation.org | Ciênsação hands-on experiments are published as Open Educational resources under a Creative Commons Attribution-ShareAlike 4.0 International License.
Measure the spectral bands of a light source…
…with this open spectrometer and…
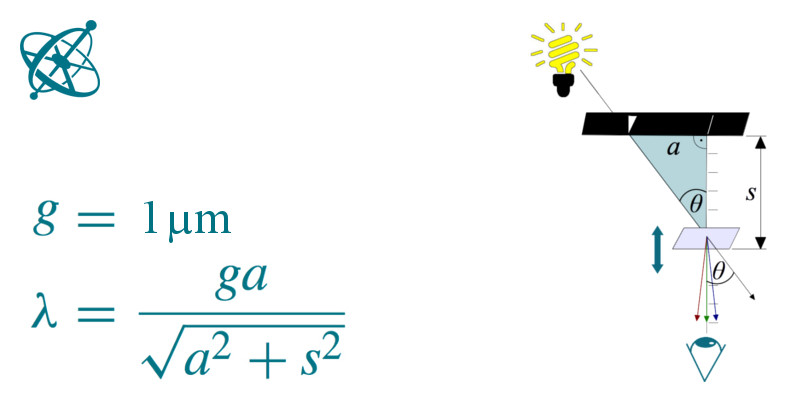
…some simple math.
Open spectrometer
Spectrometers are usually closed boxes. This spectrometer, in contrast, is literally open, and allows with simple means and basic math to measure for instance the spectral bands of a fluorescent light bulb. Some students have achieved remarkably accurate results in less than 15 minutes.
Observing the working principle of optical spectrometers.
Understanding how the diffraction on a grating is used to separate different wavelengths.
Making accurate measurements at the nanometer level.
Diffraction grating with 1000 lines per millimeter
Scissors
Translucent tape
Fluorescent light bulb
Arrange for each group a printout of the worksheet and a fluorescent table lamp. Please make sure that the worksheet is printed at exactly 100%, so that the scale on the print is accurate.
Cut out the triangular area at the top of the worksheet and cover it with translucent tape. Then fold up the dark upper part exactly at the bottom of the rectangle and make it stand upright. Place the fluorescent light, whose spectrum you want to measure, behind the triangular window. If you now hold the diffraction grating upright over the scale at 7 cm, you will see colored triangles, each the result of one of the lamp's spectral bands. To take accurate measurements, it is important to hold the diffraction grating upright and parallel to the black background, and to look along the scale toward the white line. Then move the diffraction grating back and forth along the scale until a triangle lies over the white line. Read the distance from the black background on the scale and calculate the wavelength with the formula given on the worksheet.
A detailed explanation of the spectrometer design and the underlying physics can be found in this article from IOP's Journal of Physics Education.